Análisis de los Métodos

Estudio Matemático de los métodos de resolución de los 

Sistemas de Ecuaciones

Método de sustitución:

1)      Se despeja una incógnita en una de las ecuaciones.

2)      Se sustituye el valor de esta incógnita en la otra ecuación, obteniendo una ecuación con la otra incógnita.

3)      Se resuelve la ecuación.

4)      El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada

5)      Obteniendo así la solución.
   

             

                               Método de igualación:

1) Se despeja la misma incógnita en las dos ecuaciones.

2) Se igualan las expresiones resultantes lo cual da lugar a una ecuación con una incógnita.

3) Se resuelve la ecuación.

4) El valor obtenido se sustituye en cualquiera de las dos expresiones en la que aparecía despejada la otra incógnita.

5)  Obteniendo de esta manera, la solución del sistema.

Método de reducción por suma o resta:

1) Se multiplican las ecuaciones por un número conveniente para igualar el valor absoluto de los coeficientes de una misma incógnita, en las dos ecuaciones.

2) Según sean los signos de dichos coeficientes, es decir, de igual o distinto signo, se restan o suman las ecuaciones, con lo que se consigue eliminar dicha incógnita.

3) Se resuelve la ecuación de primer grado en la otra incógnita que así resulta.

4) Se reemplaza ésta por su valor en una de las ecuaciones dadas y se obtiene el valor de la primera incógnita.

Método de determinantes o Regla de Cramer:

                  Determinante: es un número que se obtiene de hacer la diferencia del producto de las                            diagonales de una matriz cuadrada de coeficientes. Se representa como |A|.

                  Matriz: es un arreglo de números ubicados ordenadamente por filas y columnas.

                    Dado el siguiente sistema de ecuaciones y la representación de su matriz de coeficientes                                                      

                                                           

  

                 El valor de cada incógnita, es una razón, que tiene por denominador el determinante de los coeficientes de las incógnitas y por numerador el determinante que se obtiene al reemplazar en el anterior la columna de los coeficientes de la incógnita que se quiere calcular por los términos independientes.

               Veamos, si al resolver un sistema en notación generalizada con los métodos analíticos, podemos sacar alguna conclusión.

Método de igualación:

Método de sustitución:

              Si  se sustituyera la expresión al valor de “x” en la ecuación despejada en el paso 1, como indica el paso 4 en el método de sustitución, se obtendría la misma expresión que para el valor de “y” obtenida en el paso 4 del método de igualación.

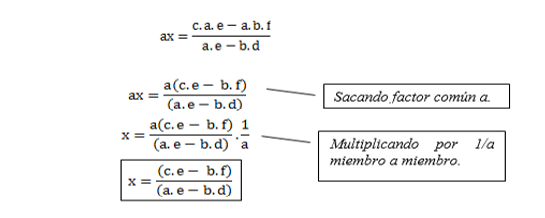
Método de reducción:

           

   

A medida que se observan las resoluciones con los distintos métodos, se observa que las expresiones para el valor de “x” e “y” siempre son iguales entre sí, por lo que se concluye que los métodos son similares, en lo que sí se diferencian es en el procedimiento para eliminar una de las incógnitas, es decir, en el método de igualación al despejar, por ejemplo, la incógnita “y” de las dos ecuaciones e igualarlas, lo que se hace es eliminar la incógnita “y” y trabajar con una ecuación con una incógnita “x”. En el método de sustitución al despejar en una de las ecuaciones “y”, y sustituir en la otra, desaparece “y”,  trabajando después con la incógnita “x”. En el método de reducción por sumas o restas, lo que se hace es transformar el sistema en un sistema equivalente efectuando la multiplicación de un número por una de las ecuaciones, de tal manera que los coeficientes de una de las incógnitas del sistema nos queden iguales u opuestos y, se resta o suma correspondientemente, logrando de esta manera la eliminación de una de las incógnitas, para luego seguir resolviendo una ecuación con una incógnita.

      

   Al resolver un sistema de  ecuaciones, mediante cualquiera de los métodos analíticos, una vez que  eliminamos, por ejemplo, la incógnita “y” y nos quede una ecuación con la incógnita “x”, puede darse las siguientes posibilidades:

1.       Que encontremos un valor para x, por ejemplo x = a.  Al sustituir este valor en una de las ecuaciones siempre obtendremos un valor para “y”. Si este es el caso los valores encontrados, de x e y, es un par ordenado que verifica ambas ecuaciones simultáneamente. Entonces, el sistema tiene una única solución y se clasifica como Compatible Determinado.

2.      Si al resolver la ecuación con una incógnita obtenemos la expresión 0. x = 0, el sistema tiene infinitas soluciones, ya que, al darle cualquier valor a x, siempre obtendremos, como resultado cero, es decir, siempre se va a verificar la igualdad. En este caso el sistema se clasifica como Compatible Indeterminado.

3.      En cambio, si obtenemos la expresión 0. x = a, siendo a¹0, el sistema no tiene solución, ya que, ningún valor multiplicado por cero dará como resultado un valor distinto de cero.